Exploring The Fascinating World Of The Perfect Heptagon

Have you ever wondered what makes a perfect heptagon so unique in geometry? A perfect heptagon is a seven-sided polygon with equal sides and angles, offering a symmetrical beauty that has fascinated mathematicians, artists, and architects for centuries. Unlike other polygons, the perfect heptagon holds a special place in mathematical studies due to its intriguing properties and the challenges it presents in construction. Its symmetry and balance make it a perfect subject for exploration in both theoretical and practical applications.

The concept of the perfect heptagon extends beyond mathematics and into the realms of art, design, and even nature. From the intricate patterns of snowflakes to the architectural marvels inspired by geometric precision, the perfect heptagon is a testament to the harmony and order found in the universe. Understanding its characteristics not only deepens our appreciation for geometry but also opens doors to creative applications in various fields.

Despite its seemingly simple structure, the perfect heptagon has complexities that continue to intrigue scholars and enthusiasts alike. Its angles, proportions, and relationships with other geometric shapes make it a cornerstone of mathematical exploration. Whether you're a student, a professional, or simply someone curious about shapes, the perfect heptagon offers a wealth of knowledge and inspiration worth exploring.

Read also:

Jennifer Stahl Unveiling The Journey Of A Remarkable Personality

What is a Perfect Heptagon?

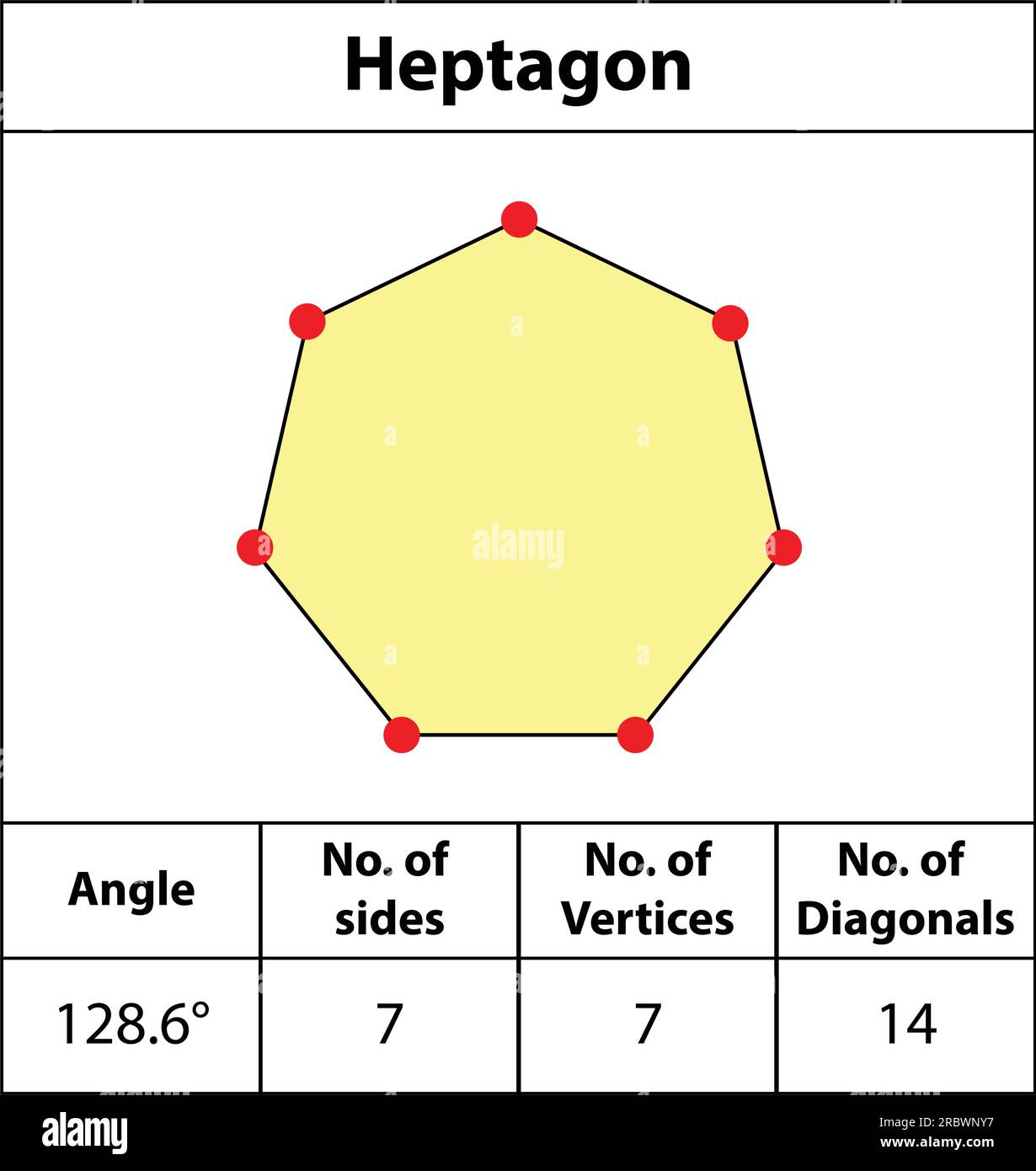
A perfect heptagon is a polygon with seven equal sides and seven equal angles, making it a regular polygon. Unlike irregular heptagons, which may have sides and angles of varying lengths, the perfect heptagon is defined by its symmetry and uniformity. Each interior angle of a perfect heptagon measures approximately 128.57 degrees, and the sum of all interior angles is 900 degrees. These precise measurements make the perfect heptagon a fascinating subject in geometry.

To better understand the perfect heptagon, consider its relationship with other regular polygons. For instance, a perfect triangle (equilateral triangle) and a perfect square are easier to construct due to their simpler geometric properties. However, the perfect heptagon presents a unique challenge because it cannot be constructed using only a compass and straightedge, a fact that has intrigued mathematicians for centuries.

Why is the Perfect Heptagon So Special?

The perfect heptagon stands out among polygons due to its complexity and the challenges it poses in geometric construction. Unlike polygons with fewer sides, such as triangles or squares, the perfect heptagon cannot be constructed using classical tools like a compass and straightedge. This limitation has led to extensive research and innovative methods for approximating its shape, making it a subject of fascination for mathematicians and engineers alike.

Beyond its mathematical intrigue, the perfect heptagon is celebrated for its aesthetic appeal. Its balanced proportions and symmetry have inspired countless works of art, architecture, and design. From intricate mosaics to modern sculptures, the perfect heptagon serves as a symbol of harmony and precision.

How Can You Draw a Perfect Heptagon?

Drawing a perfect heptagon requires precision and the right tools. While it cannot be constructed using a compass and straightedge alone, there are alternative methods to approximate its shape. One common approach involves using a protractor and ruler to measure and mark the angles and sides accurately.

Here’s a step-by-step guide to drawing a perfect heptagon:

Read also:

William Nylander Siblings A Closer Look At Their Lives And Achievements

1. Draw a circle using a compass.
2. Divide the circle into seven equal parts by marking points along its circumference.
3. Connect the points with straight lines to form the heptagon.

For those seeking more advanced techniques, computer-aided design (CAD) software can be used to create a precise perfect heptagon. This method ensures accuracy and allows for easy adjustments to the shape.

What Are the Properties of a Perfect Heptagon?

The perfect heptagon has several unique properties that distinguish it from other polygons. These include:

• Seven equal sides and angles.
• Each interior angle measures approximately 128.57 degrees.
• The sum of all interior angles is 900 degrees.
• It cannot be constructed using only a compass and straightedge.

These properties make the perfect heptagon a cornerstone of geometric exploration and a valuable tool in various fields, from mathematics to design.

Applications of the Perfect Heptagon in Real Life

The perfect heptagon finds applications in a wide range of fields, from architecture to engineering. Its symmetrical design makes it ideal for creating visually appealing structures and patterns. For example, many modern buildings incorporate heptagonal shapes to achieve a sense of balance and harmony.

In addition to architecture, the perfect heptagon is used in the design of everyday objects such as coins, tiles, and even furniture. Its unique shape adds an element of intrigue and sophistication, making it a popular choice for designers and artists.

Famous Examples of Perfect Heptagon in Architecture

One of the most famous examples of the perfect heptagon in architecture is the Mausoleum at Halicarnassus, one of the Seven Wonders of the Ancient World. This structure features a heptagonal base, showcasing the ancient world's appreciation for geometric precision.

Modern architecture also embraces the perfect heptagon. For instance, the Royal Albert Hall in London incorporates heptagonal elements in its design, creating a visually stunning and acoustically superior space.

How Does the Perfect Heptagon Relate to Nature?

Nature is full of geometric wonders, and the perfect heptagon is no exception. While it may not appear as frequently as hexagons or pentagons, the perfect heptagon can be found in certain natural formations, such as the patterns of some flowers and snowflakes.

These natural occurrences highlight the universal principles of symmetry and balance that govern the world around us. By studying the perfect heptagon in nature, scientists gain insights into the underlying patterns that shape our environment.

Common Misconceptions About Perfect Heptagons

Despite its geometric simplicity, the perfect heptagon is often misunderstood. One common misconception is that it can be constructed using only a compass and straightedge, similar to a perfect triangle or square. However, this is not the case, as the heptagon requires more advanced techniques for accurate construction.

Another misconception is that the perfect heptagon is less significant than other polygons. In reality, its unique properties and applications make it a valuable subject of study in both theoretical and practical contexts.

Tools and Techniques to Study Perfect Heptagons

Studying the perfect heptagon requires a combination of traditional and modern tools. While a protractor and ruler are sufficient for basic constructions, advanced techniques often involve the use of CAD software and mathematical algorithms.

These tools allow researchers to explore the properties of the perfect heptagon in greater detail, leading to new discoveries and applications. Whether you're a student or a professional, understanding these tools can enhance your appreciation for this remarkable shape.

Why Should You Care About the Perfect Heptagon?

The perfect heptagon is more than just a geometric shape; it is a symbol of balance, symmetry, and precision. By studying the perfect heptagon, we gain insights into the principles that govern the natural and man-made world. Its applications in art, architecture, and design demonstrate its enduring relevance and appeal.

Whether you're a mathematician, an artist, or simply someone curious about shapes, the perfect heptagon offers a wealth of knowledge and inspiration. By exploring its properties and applications, we deepen our understanding of geometry and its role in shaping the world around us.

Details

Details